It happened to me recently. I was developing the backend for a web application, and this apparently easy and trivial problem resulted to be a complicated one. It was similar to other problems I've dealt with in the past - but the solution was not the same as the one in any of those.

I tried to figure it out on my own for a while, until I gave up and decided to ask my old friend, the almighty and wise Google, if he (or she?) got the answer. It was then when it struck me. I didn't know how to search about the problem I was trying to resolve; I didn't know its name!

“Kids, let me tell you about another so called ‘wicked’ guy. He had long hair and some wild ideas, and he didn’t always do what other people thought was right, and that man’s name was . . . I forget. But the point is . . . I forget that, too. Marge, you know who I’m talking about, he used to drive that blue car.”

So I started asking Google the same questions I was asking myself:

• How to know if there exists a combination of a given set of entities that satisfies a given set of conditions?
• Matching entities with conditions
• Algorithm to know if every condition in a given set is satisfied by a unique entity from a given set

And after every search, I found no answer to my specific problem. As Homer in that Simpsons' episode, I was being too generic and giving no specific directions for the other part (Google in this case) to get where I wanted to get.

What was the problem in question?

I'll try to describe it briefly.

Given a set of people and a set of rules, I needed to know if that group of people could satisfy every one of the rules and, in the solution, each person was assigned to only one of the rules it satisfies. People were characterized by their age and gender. And each rule had a variable amount of conditions on those properties.

I also reformulated it in terms of buckets (replacing the rules) and objects (replacing the people). I had to put exactly one object in each bucket. And an object, given its shape (age and gender), could fit or not (it satisfies the rule's conditions) in a bucket. If there is a combination were each object ends up in a bucket, and each bucket has only one object inside, then that group of objects meets the necessary criteria, and a solution exists.

In my case, as in the solution sought, every person should be assigned to one rule and each rule to only one person, it only makes sense to try to find a solution if the number of elements in each set (people and rules) is the same.

What are names, in essence?

As a software developer I'm familiar, and use it periodically, with the concept of unique identifiers.

• Almost everything in the databases area (both relational and non-relational) is based on having a unique identifier to get to a specific resource (a row in a table, or an object in a collection).
• If you've worked with C (or any other low level language), you know about pointers - those peculiar entities used to reference a precise block in the system memory.

For those without programming knowledge, there are lot's of examples in everyday life. How do you tell people where you live? A complete address specifies a unique place on Earth. Every cellphone has an exclusive number to reach it. In my country, Argentina, we have the DNI (for National Identity Document, in Spanish), because people's names are not enough to uniquely single out every person.

We use this concept constantly. And when we don't know the name of something (understanding by "name" the concept of unequivocally identifying an entity), we start to use diverse tools and resources to try to achieve the same level of specificity. We might describe a person by its physical appearance, or by family or friend relationships, or by its job or studies.

I ended up using this kind of techniques to find the solution to my original dilemma. I was lucky to study at the engineering university, and back then we examined lot's of problems of various kinds and families. From combinatorial or optimization problems, to graph and networks theory. Many times the same problem had multiple solutions by approaching it from different angles or by modeling reality prioritizing another set of properties.

Because of all these situations I studied when in college, I knew that the key had to be somewhere in the realm of graph theory or similar, so I limited my search to problems of this kind, hoping to finally come to the solution I was looking for.

I started asking around to its distant relatives, like the Traveling Salesman Problem and its variations but got no luck with them.

the Traveling Salesman Problem

Some of them pointed me towards another kind of problem, like the Knapsack Problem. It looked familiar at first glance - if my entities were the things to put inside the knapsack, and conditions were some kind of capacity... But none of its mutations gave me what I wanted.

the Knapsack Problem

Transportation problems also got thrown into the mix, and it seemed a promising modeling approach. If every one of my entities was considered as a source, and every condition was considered as a destination with a capacity of 1, and if a solution was found where all sources arrived at a destination.... I was getting closer!

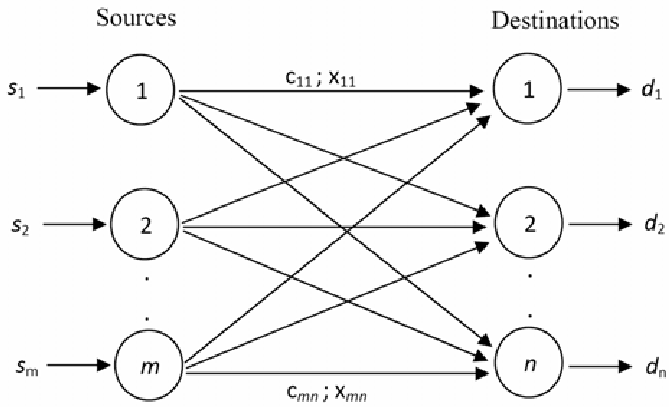
the Transportation Problem

I also dove into the ocean of Network Flow Problems and things were looking good. Very similar situations were solved using this kind of model, so it was a matter of time until I found the guy I was looking for.

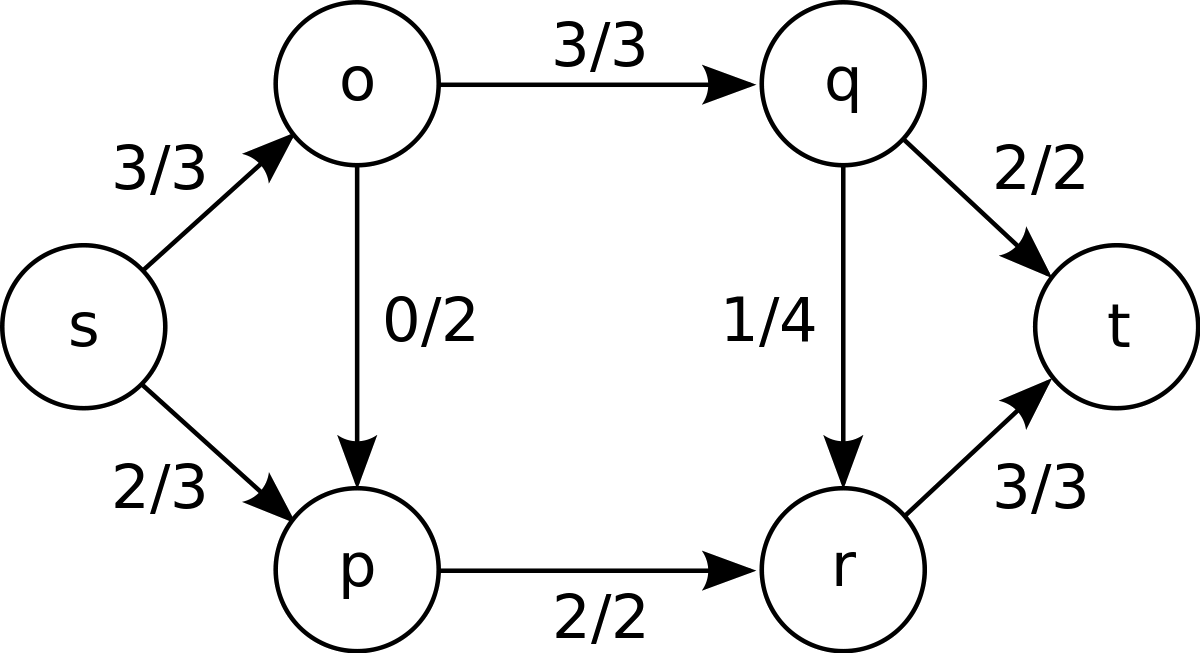
the Network Flow Problem

I finally found it

It wasn't easy. I knocked on many doors, in far-away-from-each-other neighborhoods, roaming in the universe of combinatorial theory, networks, graphs, algorithms, etc. But in the end I hit the target. The name I was looking for was Maximum Cardinality Matching in Bipartite Graphs. Given a bipartite graph the goal is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). On one set, there were my entities. And on the other, the restrictions or conditions. An edge exists between elements of different sets if the entity satisfies the condition. For my particular problem, if the maximum cardinality of the constructed graph was equal to the number of entities, then a solution can be found where each entity satisfies a different condition.

Luckily, and for my peace of mind, I was glad to find out that there are multiple algorithms for solving this riddle.

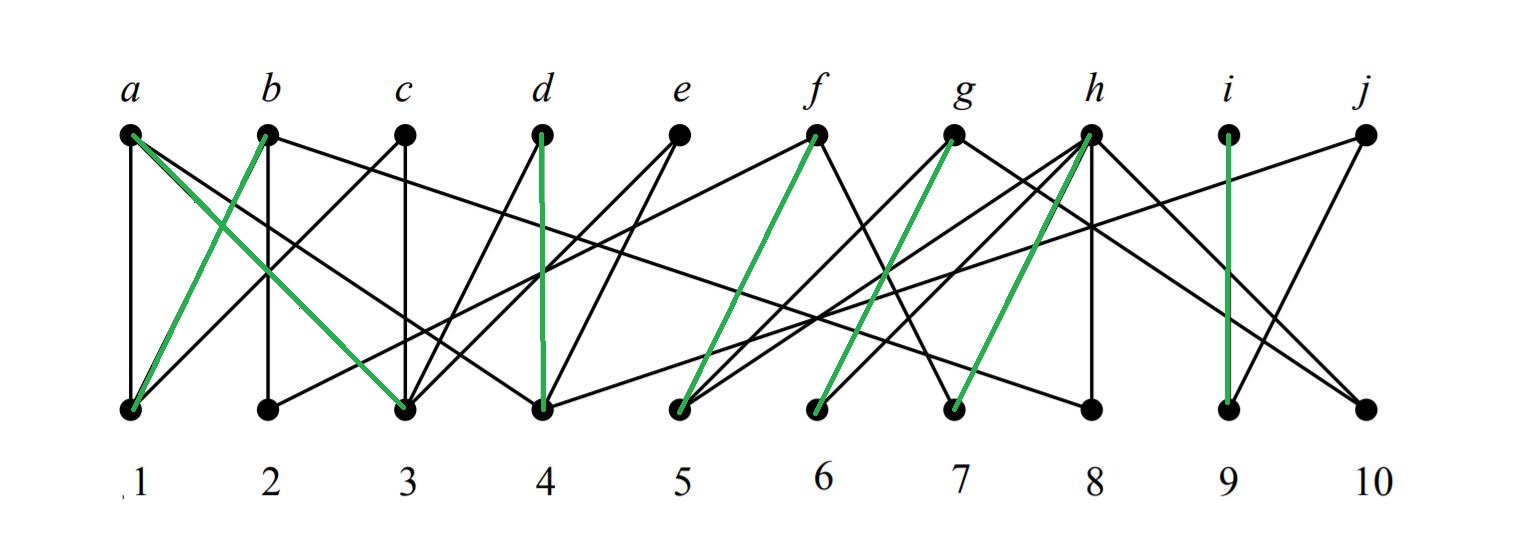
the Maximum Cardinality Matching of Bipartite Graphs problem

Of the many options for dealing with this, I opted for a pretty simple C implementation of the Ford-Fulkerson with DFS algorithm I found on the Internet, which wasn't hard to transcode to PHP. It uses matrices to model graphs and the elements of the matrix represent the existence of edges (a 1 if it exists, a 0 if it doesn't).

Curious fact: the Ford-Fulkerson algorithm actually models the problem as a network and finds the maximal flow of it, showcasing how close these two kinds of problems are.

Afterthought

It was a pretty funny ride, though not the most time-efficient business. If I had known the proper name of the problem beforehand, I would have saved a lot of time and gone directly to the solution. On the other hand, I have now made many new contacts in the world of algorithmic problems - valuable contacts I can reach out the next time I need to find someone I don't yet know.